Autores:
(1) Oleksandr Kuznetsov, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, EE. UU. y Departamento de Ciencias Políticas, Comunicación y Relaciones Internacionales, Universidad de Macerata, Via Crescimbeni, 30/32, 62100 Macerata, Italia ([email protected]);
(2) Dzianis Kanonik, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, EE.UU.;
(3) Alex Rusnak, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, EE. UU. ([email protected]);
(4) Anton Yezhov, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, EE. UU.;
(5) Oleksandr Domin, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, EE. UU.
Tabla de enlaces
Resumen y 1. Introducción
1.1 El paradigma blockchain y el desafío de la escalabilidad
1.2 Estado del arte
1.3. Nuestra contribución y 1.4. Estructura del artículo
2. Conceptualización del problema
3. Nuestra idea para optimizar árboles en blockchain
4. Eficiencia de los árboles de Merkle adaptativos
5. Algoritmo para la reestructuración del árbol de Merkle
6. Ejemplos de ejecución de algoritmos de reestructuración de árboles de Merkle y 6.1 Ejemplo 1: Reestructuración de un árbol binario mediante la adición de una hoja
6.2. Ejemplo 1.1: Reestructuración de un árbol binario mediante intercambio de nodos de hoja
6.3. Ejemplo 2.1: Reestructuración de un árbol no binario mediante la adición de una sola hoja
6.4. Ejemplo 2.2: Reestructuración de un árbol no binario mediante el intercambio de pares de hojas
6.5. Ejemplo 2.3: Reestructuración de un fragmento de árbol Patricia-Merkle mediante intercambio de pares de hojas
7. Codificación de rutas en el árbol de Merkle adaptativo
8. Mejora de los árboles Verkle mediante reestructuración adaptativa y 8.1. Aplicación de árboles adaptativos en la tecnología de árboles Verkle
8.2 Tecnología y ventajas
9. Discusión
9.1 Nuestra contribución
9.2 Comparación con soluciones existentes
10. Conclusión y referencias
2. Conceptualización del problema
El tema central abordado en esta investigación es la optimización de las estructuras de árbol en los sistemas blockchain para una verificación eficiente y rentable. Actualmente, los datos de blockchain se almacenan en árboles equilibrados, con rutas de Merkle para la verificación de datos que son aproximadamente iguales en longitud y complejidad en todos los datos. Esta uniformidad da como resultado un costo y una complejidad de verificación consistentes, independientemente de la frecuencia de uso de los datos.
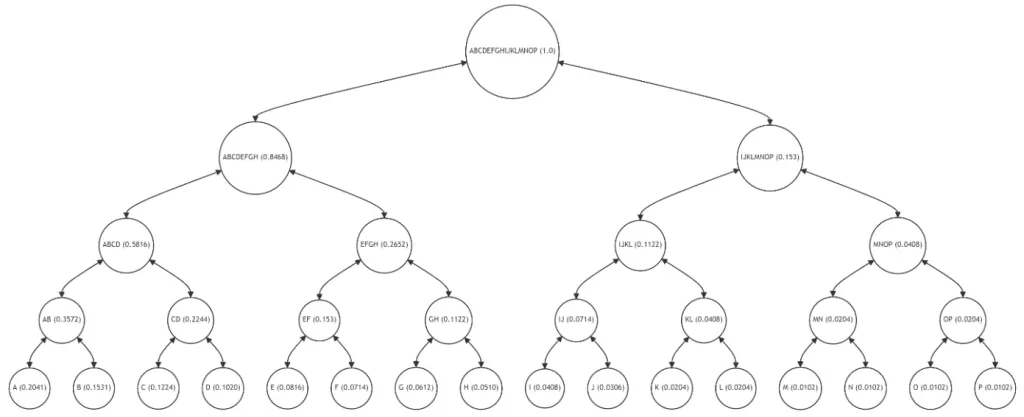
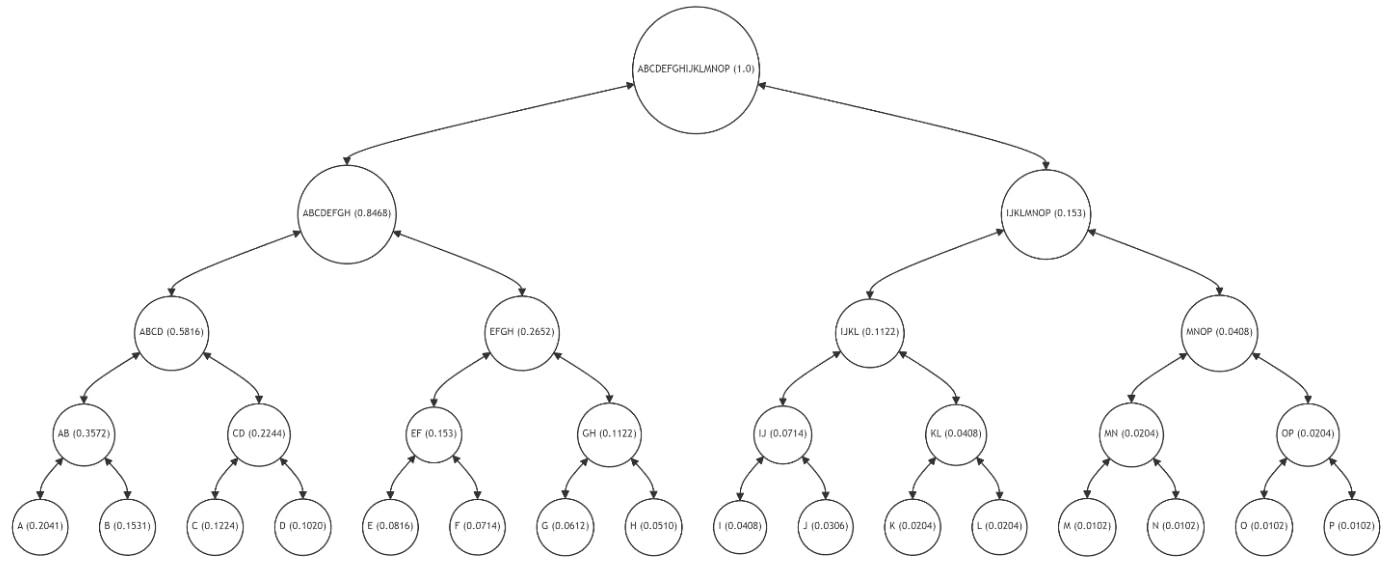
La figura 3 muestra un árbol de Merkle equilibrado, una estructura de datos fundamental utilizada en la cadena de bloques para garantizar la integridad de los datos. Cada nodo hoja (AP) representa un bloque de datos con un valor hash único, mientras que los nodos que no son hojas (AB, CD, etc.) son hashes de sus respectivos nodos secundarios. El nodo raíz (ABCDEFGHIJKLMNOP) abarca el hash de todo el árbol, lo que proporciona un único punto de referencia para la integridad de todo el conjunto de datos.
La estructura del árbol de Merkle garantiza que cualquier alteración en un único bloque de datos se pueda detectar rápidamente al recalcular los hashes a lo largo del árbol hasta la raíz. Sin embargo, esta estructura equilibrada, si bien es eficiente a la hora de distribuir los datos de manera uniforme, no tiene en cuenta la frecuencia de acceso o modificación de los datos (la frecuencia se indica entre paréntesis). Como resultado, los datos que se utilizan con frecuencia y los que se acceden con poca frecuencia tienen el mismo nivel de complejidad y costo en términos de verificación, lo que genera ineficiencias en la utilización de los recursos.
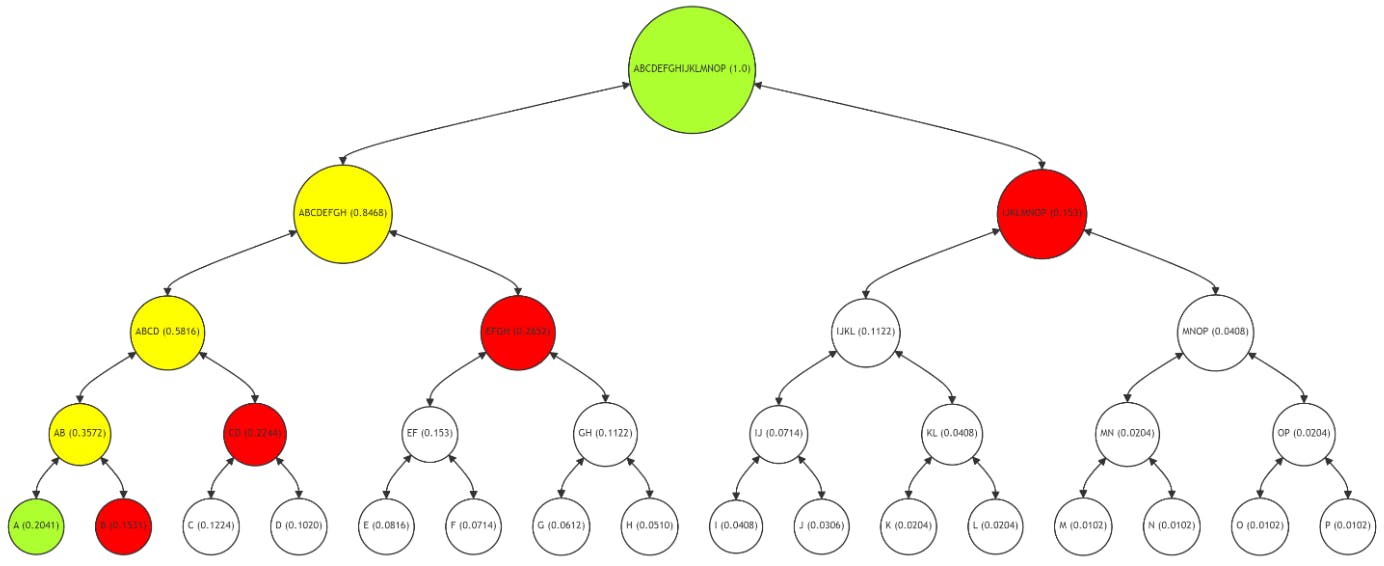
La Figura 4 resalta la ruta de Merkle (nodos B, CD, EFGH, IJKLMNOP) para verificar la integridad del nodo hoja A (con una alta frecuencia de 0,2041). La ruta de Merkle está marcada en rojo, lo que indica los nodos cuyos hashes son necesarios para verificar la integridad de A hasta la raíz. El nodo hoja A y la raíz están resaltados en verde, mientras que los nodos intermedios (AB, ABCD, ABCDEFGH) involucrados en los cálculos de hash están en amarillo.
El proceso de verificación implica volver a calcular y comparar los hashes desde el nodo A hasta la raíz, lo que garantiza la integridad de los datos. Sin embargo, este método, aunque sencillo, aplica la misma complejidad de verificación a todos los datos, independientemente de la frecuencia de uso. Este enfoque de «talla única» no es óptimo, especialmente para los datos a los que se accede y modifica con frecuencia, ya que genera una sobrecarga computacional innecesaria.
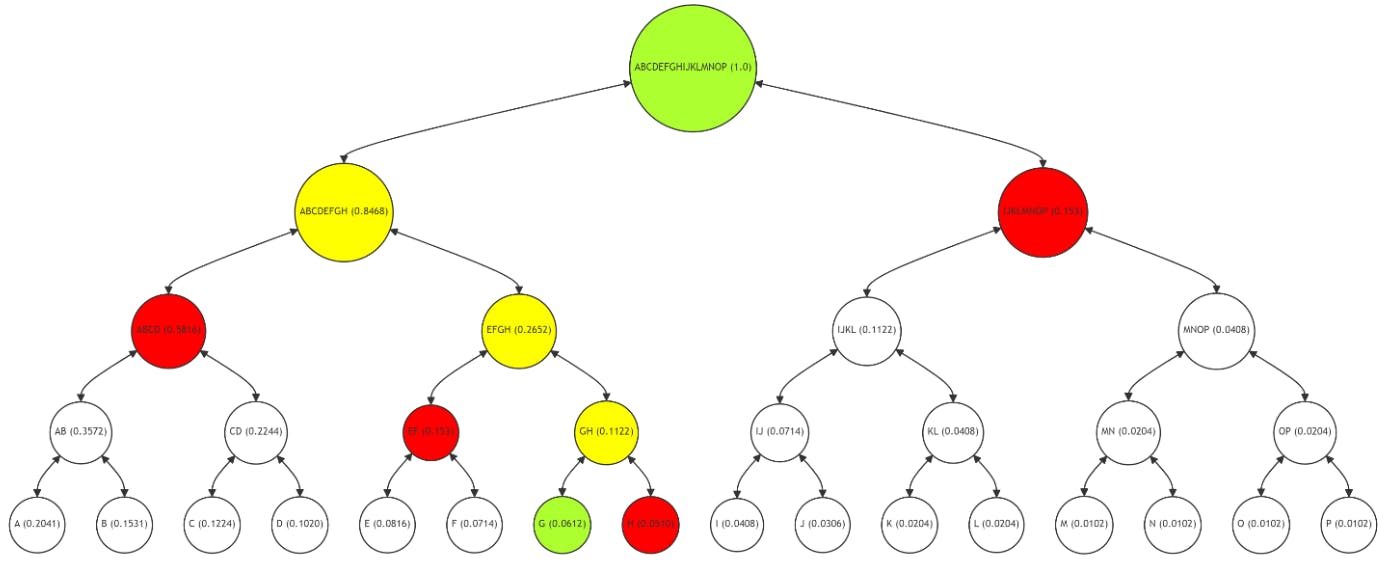
En la Figura 5, se muestra la ruta de Merkle para verificar el nodo hoja G (con una frecuencia de 0,0612). La ruta (nodos H, EF, ABCD, IJKLMNOP) está marcada en rojo, con el nodo G y la raíz en verde, y los nodos intermedios (GH, EFGH, ABCDEFGH) en amarillo. El proceso de verificación para G sigue el mismo principio que para A, recalculando los hashes a lo largo de la ruta roja para validar la integridad de los datos.
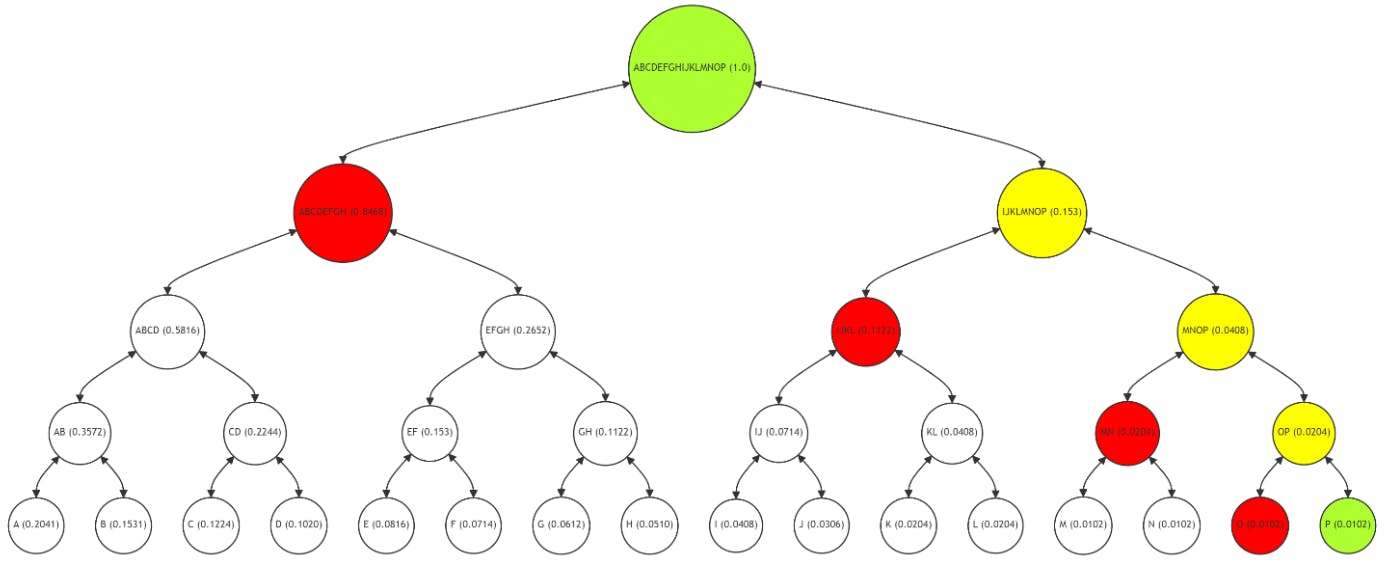
La Figura 6 muestra la ruta de Merkle para el nodo de hoja P (con una frecuencia de 0,0102), con la ruta (nodos O, MN, IJKL, ABCDEFGH) en rojo, P y la raíz en verde, y los nodos intermedios (OP, MNOP, IJKLMNOP) en amarillo. El proceso para verificar la integridad de P refleja el de A y G, lo que enfatiza el enfoque consistente en todo el árbol.
Esta coherencia en la verificación, si bien garantiza controles uniformes de seguridad e integridad, no tiene en cuenta las distintas frecuencias de acceso y modificación de los datos, lo que genera un sistema rígido y a veces ineficiente, especialmente en un entorno dinámico como el de la cadena de bloques, donde los patrones de acceso a los datos pueden variar significativamente.
Por lo tanto, el proceso actual de verificación de árboles de Merkle, como se ilustra en estas figuras, es un enfoque bastante primitivo y burdo. Trata todos los datos por igual, independientemente de su frecuencia de uso, lo que conduce a posibles ineficiencias en los recursos computacionales. Nuestra solución propuesta tiene como objetivo revolucionar este proceso mediante la introducción de árboles de Merkle adaptativos. Estos árboles optimizarán las rutas de verificación en función de la frecuencia de uso de los datos, lo que reducirá significativamente la complejidad y el costo de verificar los datos a los que se accede con frecuencia. Este enfoque innovador promete mejorar la eficiencia y la escalabilidad de los sistemas de cadena de bloques, adaptando el proceso de verificación a las necesidades dinámicas de la red. Al diferenciar entre datos a los que se accede con frecuencia y a los que se accede con poca frecuencia, los árboles de Merkle adaptativos pueden asignar recursos computacionales de manera más efectiva, lo que garantiza una verificación de datos más rápida y rentable. Este método no solo optimiza el rendimiento de la cadena de bloques, sino que también se alinea con la naturaleza cambiante del uso de la cadena de bloques, donde ciertos nodos de datos pueden convertirse en puntos calientes de actividad.
Este artículo está disponible en arxiv bajo la licencia CC by 4.0 Deed (Attribution 4.0 International).