Autores:
(1) Oleksandr Kuznetsov, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, EE. UU. y Departamento de Ciencias Políticas, Comunicación y Relaciones Internacionales, Universidad de Macerata, Via Crescimbeni, 30/32, 62100 Macerata, Italia ([email protected]);
(2) Dzianis Kanonik, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, EE.UU.;
(3) Alex Rusnak, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, EE. UU. ([email protected]);
(4) Anton Yezhov, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, EE. UU.;
(5) Oleksandr Domin, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, EE. UU.
Tabla de enlaces
Resumen y 1. Introducción
1.1 El paradigma blockchain y el desafío de la escalabilidad
1.2 Estado del arte
1.3. Nuestra contribución y 1.4. Estructura del artículo
2. Conceptualización del problema
3. Nuestra idea para optimizar árboles en blockchain
4. Eficiencia de los árboles de Merkle adaptativos
5. Algoritmo para la reestructuración del árbol de Merkle
6. Ejemplos de ejecución de algoritmos de reestructuración de árboles de Merkle y 6.1 Ejemplo 1: Reestructuración de un árbol binario mediante la adición de una hoja
6.2. Ejemplo 1.1: Reestructuración de un árbol binario mediante intercambio de nodos de hoja
6.3. Ejemplo 2.1: Reestructuración de un árbol no binario mediante la adición de una sola hoja
6.4. Ejemplo 2.2: Reestructuración de un árbol no binario mediante el intercambio de pares de hojas
6.5. Ejemplo 2.3: Reestructuración de un fragmento de árbol Patricia-Merkle mediante intercambio de pares de hojas
7. Codificación de rutas en el árbol de Merkle adaptativo
8. Mejora de los árboles Verkle mediante reestructuración adaptativa y 8.1. Aplicación de árboles adaptativos en la tecnología de árboles Verkle
8.2 Tecnología y ventajas
9. Discusión
9.1 Nuestra contribución
9.2 Comparación con soluciones existentes
10. Conclusión y referencias
3. Nuestra idea para optimizar árboles en blockchain
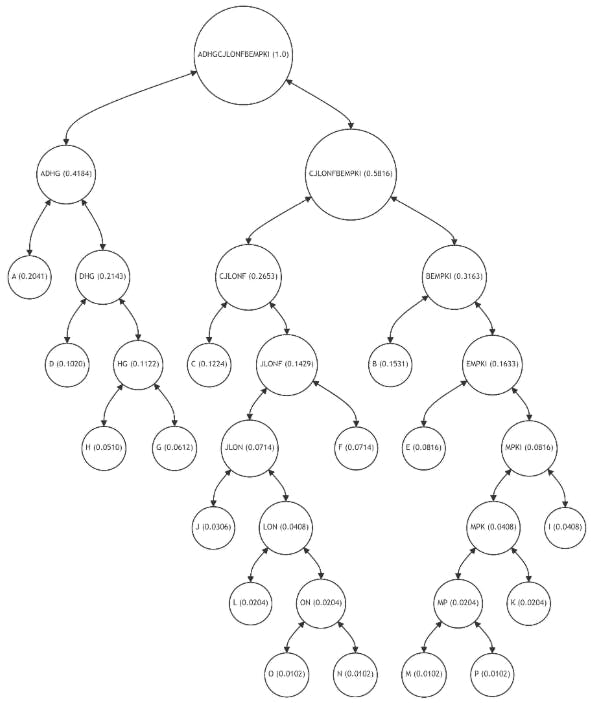
La figura 7 representa una adaptación innovadora del árbol Merkle tradicional, que incorpora los principios de codificación estadística de Shannon-Fano y Huffman. A diferencia del árbol Merkle equilibrado, esta estructura adaptativa está desequilibrada intencionalmente para optimizar el proceso de verificación en función de la frecuencia de uso de los datos. Cada nodo de hoja (PA) sigue representando un bloque de datos con un valor hash único, pero su ubicación en el árbol ahora se correlaciona con la probabilidad de su uso.
En este árbol de Merkle adaptativo, los nodos de datos más utilizados (A, B, C, D) se ubican más cerca de la raíz, lo que acorta significativamente el camino necesario para su verificación. Esta ubicación estratégica reduce la complejidad computacional y el tiempo necesarios para verificar los datos a los que se accede con frecuencia. Por el contrario, los nodos de datos menos utilizados (M, N, O, P) se ubican más lejos de la raíz, lo que refleja su menor probabilidad de acceso.
La estructura de este árbol es una aplicación directa de los principios de codificación de Shannon-Fano y Huffman, donde a los elementos más comunes se les asignan códigos más cortos (o rutas en el caso de un árbol de Merkle). Este enfoque garantiza que la longitud promedio de la ruta para la verificación se minimice, alineando el esfuerzo computacional con los patrones de uso reales de los datos dentro de la cadena de bloques.
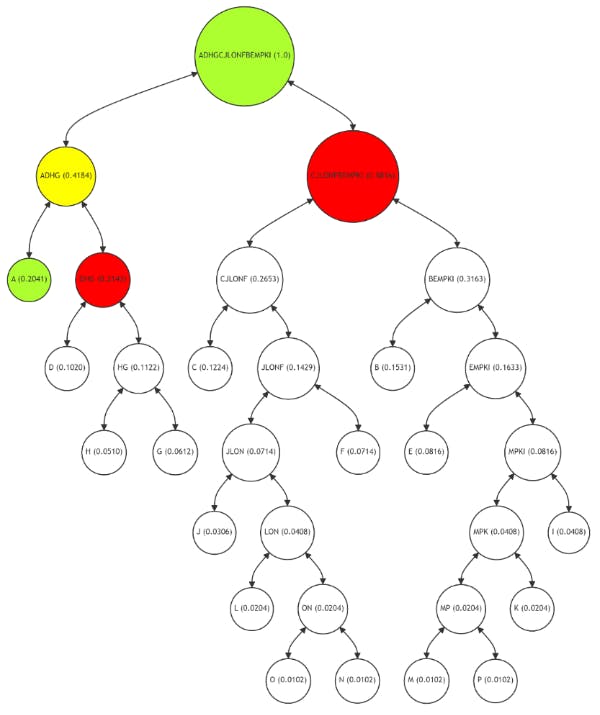
En la Figura 8, la ruta de Merkle para el nodo de hoja A (resaltado en verde) es significativamente más corta que en un árbol de Merkle equilibrado. La ruta (marcada en rojo) incluye los nodos DHG y CJLONFBEMPKI, con cálculos intermedios (en amarillo) en el nodo ADHG. Esta ruta optimizada refleja la alta frecuencia de uso del nodo A, lo que hace que el proceso de verificación sea más rápido y más rentable. La integridad del nodo A se puede verificar con menos pasos computacionales, lo que demuestra la eficiencia del árbol de Merkle adaptativo en el manejo de datos de uso frecuente.
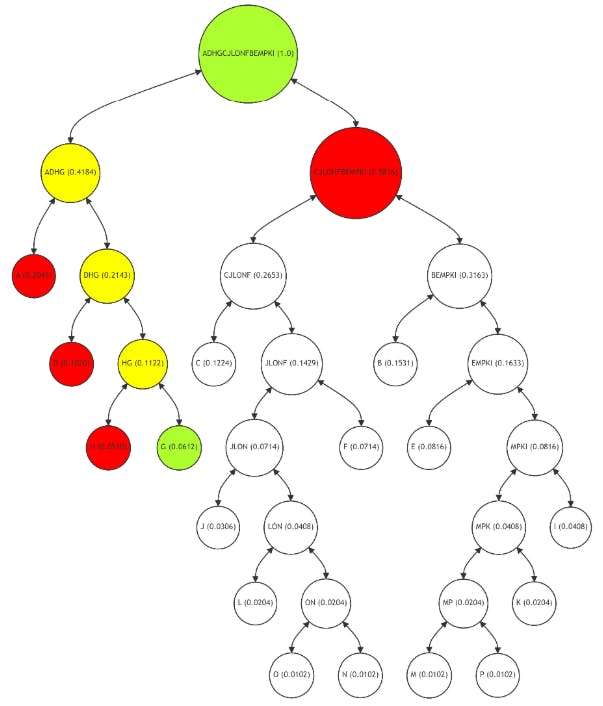
Para el nodo de hoja G (Figura 9), la ruta de Merkle incluye los nodos H, D y CJLONFBEMPKI, con cálculos intermedios en los nodos HG y ADHG. Esta ruta, si bien es más larga que la del nodo A, aún está optimizada en función de la frecuencia de uso de G. La estructura de árbol adaptativa garantiza que el proceso de verificación siga siendo eficiente, incluso para nodos con un uso moderado. Este enfoque equilibra la necesidad de integridad de los datos con la eficiencia computacional, adaptando la complejidad de la verificación al patrón de uso de cada nodo.
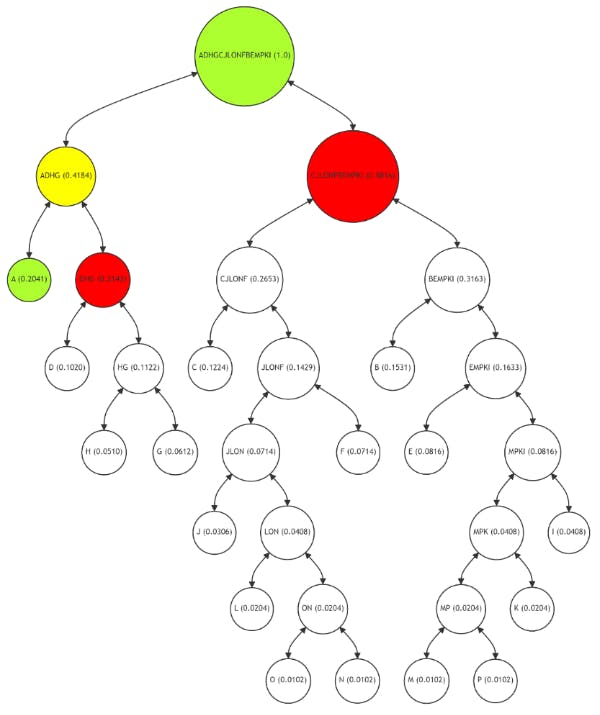
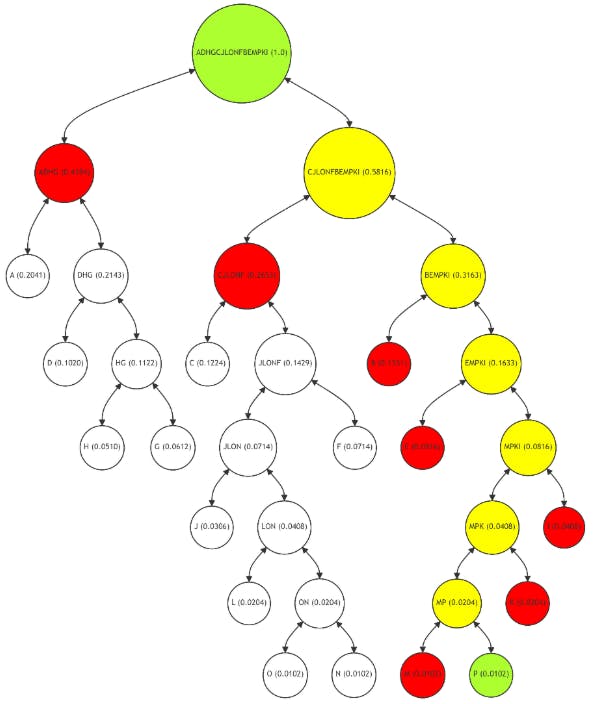
La ruta de Merkle para el nodo de hoja P (Figura 10), un nodo que se usa con menos frecuencia, es más larga e incluye los nodos M, K, I, E, B, CJLONF y ADHG. La ruta refleja la menor frecuencia de uso de P, con más cálculos intermedios (nodos MP, MPK, MPKI, EMPKI, BEMPKI y CJLONFBEMPKI) necesarios para la verificación. Si bien esto hace que el proceso de verificación para P requiera más recursos, se justifica por el uso poco frecuente del nodo. Este ejemplo ilustra cómo el árbol de Merkle adaptativo asigna recursos computacionales de manera más eficiente, centrándose en optimizar las rutas para los nodos que se usan con más frecuencia.
Por lo tanto, el enfoque del árbol de Merkle adaptativo mejora significativamente la eficiencia de la verificación de datos en los sistemas de cadena de bloques. Para los nodos de alta frecuencia como A, el proceso de verificación se simplifica y requiere menos pasos computacionales y recursos. Esta optimización puede llevar a un proceso de verificación que es hasta dos veces más rápido y rentable en comparación con un árbol de Merkle equilibrado. Por el contrario, para los nodos con frecuencias de uso más bajas, como P, la ruta de verificación más larga es una compensación razonable, considerando su acceso poco frecuente.
Este artículo está disponible en arxiv bajo la licencia CC by 4.0 Deed (Attribution 4.0 International).