La Tabla 4 resume las notaciones utilizadas en este artículo. Como se muestra en la Fig. 4, hay dos módulos principales en nuestro esquema. La primera es la Fase de Creación y Registro de Identidad y la segunda es la Fase de Autenticación de Identidad.
Diseño de protocolo
Supongamos que el usuario Ud. quiere iniciar sesión en un proveedor de servicios \(S_p\) usando el sistema blockchain [Ethereum (\(IdP_Eth\)) or Hyperledger Fabric (\(IdP_HLF\))]. Hay dos fases clave para realizar esto.
Fase de creación y registro de identidad.
Inicialmente, se crea una identidad válida para el usuario que cumple con los estándares DID del W3C. Luego viene la fase de registro de usuario. Los detalles se elaboran de la siguiente manera.
-
1.
Ud. envía los detalles (\(Nombre || Correo electrónico\_ID || SSN || Sangre\_Grupo || Nacimiento\_Fecha || Teléfono\_Número\)) hacia \(W_Aplicación\) para la creación del HIZO que cumple con los estándares W3C DID.
-
2.
El HIZO luego se pasa a un esquema (1,3,4) \(SSH_generar\) para generar cuatro acciones (\(DID_ MS, DID_ S2, DID_ S3, DID_ S4) \) según el Algoritmo 1, del cual la primera acción es obligatoria para regenerar el HIZO.
-
3.
El \(DID_ MS \) es la acción importante que podría revelar el DID al combinarla con dos de las tres acciones restantes. Esto debe mantenerse privado y seguro por parte del Ud..
-
4.
las tres acciones \(DID_ S2, DID_ S3, DID_ S4 \) se almacenan en el IPFS. Ahora se puede acceder a estas acciones con sus valores hash. \(IPFS_Hash(DID_S2), IPFS_Hash(DID_S3), IPFS_Hash(DID_S4)\).
-
5.
Finalmente, \((Hash(DID) || Hash(DID_MS) || IPFS_Hash(DID_S2) || IPFS_Hash(DID_S3) || IPFS_Hash(DID_S4) ))\) se envían a Blockchain a través del contrato inteligente/código de cadena por parte del \(W_Aplicación\).
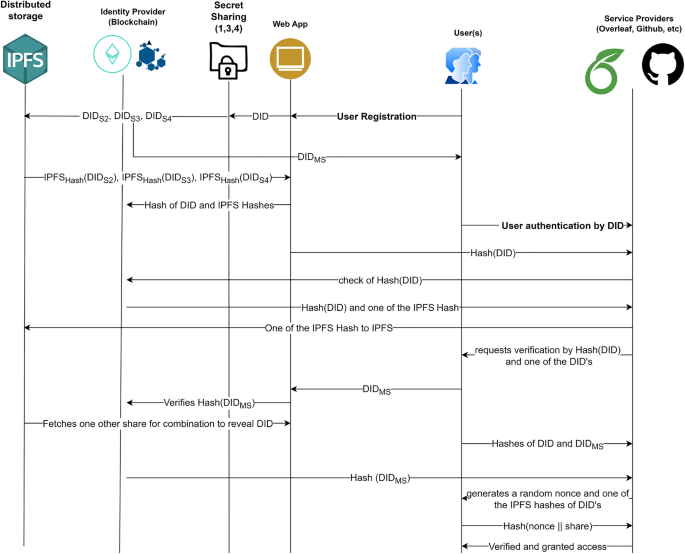
Fase de autenticación de identidad
En esta fase, el Usuario Ud. utilizará la Identidad Descentralizada (HIZO) para realizar el inicio de sesión único en el Proveedor de servicios (\(S_p\)).
-
1.
Ud. visita el \(S_p\)‘s \(W_Aplicación\) e inicie sesión usando \(IdP_Eth\) o \(IdP_HLF\) y proporciona la HIZO.
-
2.
El \(W_Aplicación\) calcula el Picadillo(HIZO) y enviado al \(S_p\).
-
3.
\(S_p\) ahora verifica el Picadillo(HIZO) de Blockchain para confirmar la existencia del usuario válido.
-
4.
Si el proporcionado HIZO pertenece al válido Ud.entonces (\(Hash(DID) || OneOf(IPFS_Hash(DID_S2), IPFS_Hash(DID_S3), IPFS_Hash(DID_S4)))\) es proporcionado por Blcockchain al \(S_p\).
-
5.
\(S_p\) ahora usa \(OneOf(IPFS_Hash(DID_S2), IPFS_Hash(DID_S3), IPFS_Hash(DID_S4))\) para recuperar una de las acciones del IPFS.
-
6.
\(S_p\) solicitud de verificación de Ud. proporcionando \((Hash(DID) || UnoDe(DID_S2, DID_S3, DID_S4))\).
-
7.
Ud. ahora usa el \(DID_ MS \) similar a una clave privada o contraseña para autenticar y enviar la misma. El \(W_Aplicación\) calcula el \(Hash(DID_MS)\) para verificarlo desde Blockchain.
-
8.
Si se encuentra que el hash coincide, entonces el \(W_Aplicación\) recupera otro recurso compartido de IPFS y realiza una operación combinada, \(SSH_Combine(DID_MS, OneOf(DID_S2, DID_S3, DID_S4), Otro(DID_S2, DID_S3, DID_S4))\) para revelar el HIZO como se indica en el algoritmo 2.
-
9.
El Ud. ahora comparte el \((Hash_Calculado(DID) || Hash(DID_MS))\) hacia \(S_p\).
-
10.
\(S_p\) ahora verifica el \(Hash(DID_MS)\) de Blockchain y verifica \(Hash_Calculado(DID)\) por Ud. es igual que Picadillo(HIZO) obtuvo inicialmente, verificando así con éxito la Ud..
-
11.
El \(S_p\) ahora generará un nonce aleatorio (\(\omega\)) y enviar \((\omega || Uno de (IPFS_ Hash (DID_ S2), IPFS_ Hash (DID_ S3), IPFS_ Hash (DID_ S4)) \) hacia Ud..
-
12.
El Ud. ahora usa \(OneOf(IPFS_Hash(DID_S2), IPFS_Hash(DID_S3), IPFS_Hash(DID_S4))\)para recuperar una de las acciones del IPFS según lo indicado por \(S_p\)y \(Hash(\omega + OneOf(Compartir))\) se calcula. Este valor hash calculado (\(Hash_Nonce+Compartir\)) se devuelve al \(S_p\).
-
13.
\(S_p\) ahora verifica (\(Hash_Nonce+Compartir\)), proporcionando así verificación multifactorial.
En la fase de creación y registro de identidad, utilizamos contratos inteligentes (o código de cadena) para almacenar los hashes de las acciones en la cadena de bloques Ethereum (o Hyperledger Fabric). En la fase de autenticación de identidad, la aplicación web recupera las acciones de Blockchain utilizando el contrato inteligente o el código de cadena. La generación de acciones y la reconstrucción secreta (es decir, los algoritmos 1 y 2) son cálculos fuera de la cadena. En nuestro modelo propuesto, hemos utilizado la programación Solidity para escribir el contrato inteligente e implementar la aplicación en Ethereum Ropsten Test Network Permissionless Blockchain. Hemos implementado el código de cadena escrito en Go Language para Hyperledger Fabric Permissioned Blockchain. Web3.js se utilizó para interconectar la interfaz de usuario con los contratos inteligentes de Blockchain.
Algoritmo clave: esquema de intercambio de secretos
Un esquema de intercambio de secretos (SSS) es un método criptográfico para dividir un secreto en varias partes y distribuirlo entre los participantes. El comerciante distribuye el secreto al norte participantes como acciones; cuando se cumple la condición requerida (un grupo de t participantes que es un conjunto en el conjunto calificado – \(\Gamma _\textitCalidad\) unido), el secreto se puede reconstruir a partir de las acciones. Este sistema se llama (t, norte) -esquema de intercambio secreto. Aquí39el menor número de acciones tllamado umbral, debería ser requerido para reconstruir el secreto. Un adversario que descubra acciones inferiores al umbral no podrá obtener el secreto asegurado. Blakley40 Utilizó un enfoque geométrico para compartir el secreto entre los participantes. Según este método, la clave secreta es el punto en el t- espacio dimensional en el que se cruzarán todos los hiperplanos. Los esquemas de intercambio secreto son beneficiosos para almacenar datos altamente confidenciales, claves de cifrado y códigos de lanzamiento de misiles. Al distribuir los datos entre los participantes, cada individuo tiene comando y control sobre los datos, minimizando así la pérdida de datos debido a un único punto de falla.
Usamos un ideal (1, t, norte)-SSS para implementar nuestro marco. Denotemos el conjunto de participantes como PAG = \(\textitp_1, \textitp_2, \textitp_3,\ldots , \textitp_\textitn\). Un SSS con un conjunto mínimo calificado \(\Gamma _\textitQM\) = \)=t con \(\textitp_1\) como se llama al participante esencial (1, t, norte)-SSS. arumugam et al.41 en 2014 propuso el acceso fuerte basado en estructura (1, t, norte)-SSS, que es un caso especial de Ateniese et al.42 construcción. Por reconstruir el secreto exacto sin ningún cambio, Cimato et al.43 en 2004, desarrolló un SSS ideal utilizando tanto OR como NOT como operaciones de reconstrucción. En este artículo utilizamos el ideal (1, t, norte)-construcciones SSS44 desarrollado por Praveen et al. en 2017. Demostramos nuestros experimentos para (1, 3, 4) -SSS.

A continuación se muestra un ejemplo de (1, 3, 4) -SSS para compartir 0 y 1 bit. Dejar PAG \(= \\textitp_1, \textitp_2, \textitp_3, \textitp_4\\) ser el conjunto de participantes. Las matrices base \(\textitT_0 (\)resp.\(\textitT_1)\) utilizados para compartir el bit 0 (resp. 1) se dan como \(\textitT_0 = \izquierda[ \beginarraycccccc 0 & 0 & 0 & 1 & 1 & 1\\ 0 & 1 & 1 & 1 & 0 & 1\\ 0 & 1 & 1 & 1 & 1 & 0 \\ 0 & 1 & 1 & 0 & 1 & 1 \\ \endarray\right]\) y \(\textitT_1 = \izquierda[ \beginarraycccccc 0 & 0 & 0 & 1 & 1 & 1\\ 1 & 0 & 1 & 0 & 1 & 1\\ 1 & 1 & 0 & 0 & 1 & 1 \\ 0 & 1 & 1 & 0 & 1 & 1 \\ \endarray\right]\). Dejemos que los datos (por ejemplo: DID) que vamos a compartir se representen como una matriz. HIZO \(= \izquierda[ \beginarraycc 1 & 0 \\ 0 & 1 \\ \endarray\right]\). Cualquier permutación de columnas de la matriz. \(\textitT_0 (\)resp. \(\textitT_1)\) se puede utilizar para construir acciones para el bit 0 (resp. 1). El conjunto mínimo calificado para (1, 3, 4) -SSS es \(\Gamma _\textitQM = \\\textitp_1,\textitp_2,\textitp_3\, \\ textitp_1,\textitp_2,\textitp_4\, \\textitp_1,\textitp_ 3,\textitp_4\, \\textitp_1, \textitp_2, \textitp_3,\textit p_4\\\). Para \(\Gamma _\textitQM\) A continuación se muestran seis acciones de cada participante generadas mediante el algoritmo 1.
\(DID_ MS \)es decir, acciones obligatorias \(\textitCSh_(1, 1) = \textitCSh_(1, 2) = \textitCSh_(1, 3) = \left[ \beginarraycc 0 & 0 \\ 0 & 0 \\ \endarray\right]\), \(\textitCSh_(1, 4) = \textitCSh_(1, 5) = \textitCSh_(1, 6) = \left[ \beginarraycc 1 & 1 \\ 1 & 1 \\ \endarray\right]\) se distribuyen a \(\textitp_1\).
\(DID_ S2 \)es decir, acciones \(\textitCSh_(2, 1) = \izquierda[ \beginarraycc 1 & 0 \\ 0 & 1 \\ \endarray\right]\), \(\textitCSh_(2, 2) = \izquierda[ \beginarraycc 0 & 1 \\ 1 & 0 \\ \endarray\right]\), \(\textitCSh_(2, 3) = \izquierda[ \beginarraycc 1 & 1 \\ 1 & 1 \\ \endarray\right]\), \(\textitCSh_(2, 4) = \izquierda[ \beginarraycc 0 & 1 \\ 1 & 0 \\ \endarray\right]\), \(\textitCSh_(2, 5) = \izquierda[ \beginarraycc 1 & 0 \\ 0 & 1 \\ \endarray\right]\) y \(\textitCSh_(2, 6) = \izquierda[ \beginarraycc 1 & 1 \\ 1 & 1 \\ \endarray\right]\) se distribuyen a \(\textitp_2\).
\(HIZO_S3\)es decir, acciones \(\textitCSh_(3, 1) = \izquierda[ \beginarraycc 1 & 0 \\ 0 & 1 \\ \endarray\right]\), \(\textitCSh_(3, 2) = \izquierda[ \beginarraycc 1 & 1 \\ 1 & 1 \\ \endarray\right]\), \(\textitCSh_(3, 3) = \izquierda[ \beginarraycc 0 & 1 \\ 1 & 0 \\ \endarray\right]\), \(\textitCSh_(3, 4) = \izquierda[ \beginarraycc 0 & 1 \\ 1 & 0 \\ \endarray\right]\), \(\textitCSh_(3, 5) = \izquierda[ \beginarraycc 1 & 1 \\ 1 & 1 \\ \endarray\right]\) y \(\textitCSh_(3, 6) = \izquierda[ \beginarraycc 1 & 0 \\ 0 & 1 \\ \endarray\right]\) se distribuyen a \(\textitp_3\).
\(DID_ S4 \)es decir, acciones \(\textitCSh_(4, 1) = \izquierda[ \beginarraycc 0 & 0 \\ 0 & 0 \\ \endarray\right]\), \(\textitCSh_(4, 2) = \izquierda[ \beginarraycc 1 & 1 \\ 1 & 1 \\ \endarray\right]\), \(\textitCSh_(4, 3) = \izquierda[ \beginarraycc 1 & 1 \\ 1 & 1 \\ \endarray\right]\), \(\textitCSh_(4, 4) = \izquierda[ \beginarraycc 0 & 0 \\ 0 & 0 \\ \endarray\right]\), \(\textitCSh_(4, 5) = \izquierda[ \beginarraycc 1 & 1 \\ 1 & 1 \\ \endarray\right]\) y \(\textitCSh_(4, 6) = \izquierda[ \beginarraycc 1 & 1 \\ 1 & 1 \\ \endarray\right]\) se distribuyen a \(\textitp_4\).

El procedimiento que se proporciona a continuación según el algoritmo 2 se utiliza para reconstruir HIZO. denotemos \(\bigotes\) como operación booleana OR y \(\bigodot\) como operación booleana AND. Según SSS, los participantes en cualquiera de los conjuntos calificados de \(\Gamma _\textitQM\) puede reconstruir un secreto. Así que aquí en este ejemplo, el conjunto calificado que seleccionamos es \(\\textitp_1,\textitp_2,\textitp_3\\) en el \(\Gamma _\textitQM\). Entonces la reconstrucción de HIZO utilizando las acciones de los participantes \(\textitp_\textit1\), \(\textitp_\textit2\) y \(\textitp_\textit3\) se da de la siguiente manera. Primero, genera todo \(\Delta _\textitj\) utilizando XOR bit a bit de las acciones de los participantes, es decir \(\Delta _1 = \bigotimes \limits _u=1^3\textitCSh_(u, 1)=\left[ \beginarraycc 1 & 0 \\ 0 & 1 \\ \endarray\right]\), \(\Delta _2 = \bigotimes \limits _u=1^3\textitCSh_(u, 2)= \left[ \beginarraycc 1 & 1 \\ 1 & 1 \\ \endarray\right]\), \(\Delta _3 = \bigotimes \limits _u=1^3\textitCSh_(u, 3)= \left[ \beginarraycc 1 & 1 \\ 1 & 1 \\ \endarray\right]\), \(\Delta _4 = \bigotimes \limits _u=1^3\textitCSh_(u, 4)= \left[ \beginarraycc 1 & 1 \\ 1 & 1 \\ \endarray\right]\), \(\Delta _5 = \bigotimes \limits _u=1^3\textitCSh_(u, 5)= \left[ \beginarraycc 1 & 1 \\ 1 & 1 \\ \endarray\right]\) y \(\Delta _6 = \bigotimes \limits _u=1^3\textitCSh_(u, 6)= \left[ \beginarraycc 1 & 1 \\ 1 & 1 \\ \endarray\right]\). Ahora el DID se obtiene aplicando la operación AND bit a bit de todos \(\Delta _\textitj\)es decir \(DID = \bigodot \limits _j=1^6\Delta _\textitj=\left[ \beginarraycc 1 & 0 \\ 0 & 1 \\ \endarray\right]\).