En el ámbito de la criptografía, particularmente cuando se trabaja con curvas elípticas, se vuelve esencial una comprensión fundamental de la aritmética modular. Al operar dentro de un campo finito, este concepto matemático juega un papel crucial para garantizar la seguridad y eficiencia de los algoritmos criptográficos. En esta sección, nos embarcaremos en una exploración de la aritmética modular, su relevancia en contextos criptográficos y la importancia de presentar este concepto a estudiantes de diversos orígenes académicos.
Al profundizar en la criptografía de curvas elípticas, los profesionales a menudo se encuentran operando dentro de un campo finito. Aquí resulta indispensable tener conocimientos de aritmética modular. Si bien los estudiantes de matemáticas e informática están familiarizados con este tipo de estructuras algebraicas, es posible que los de ingeniería, ciencias y economía no se hayan encontrado con este concepto antes. Por lo tanto, una introducción completa se vuelve imperativa.
1.1 Desafíos e importancia de la aritmética modular
Comprender la aritmética modular puede plantear desafíos para los estudiantes, ya que introduce situaciones aparentemente poco convencionales, como que 1 + 1 equivale a 0 en ciertos casos. Además, conceptos como relaciones de equivalencia y conjuntos de cocientes pueden ser complejos. Para facilitar una comprensión fluida, es fundamental complementar la introducción con numerosos ejemplos y ejercicios.
Para allanar el camino para la aritmética modular, la introducción comienza con las relaciones de equivalencia, un concepto familiar para estudiantes de diversas disciplinas. El objetivo es establecer una conexión clara entre estas nociones matemáticas abstractas y ejemplos del mundo real que los estudiantes puedan haber encontrado antes.
2.1 Equivalencia binaria en fracciones equivalentes
Uno de los primeros encuentros con las relaciones de equivalencia ocurre cuando los estudiantes exploran fracciones equivalentes. Existen conjuntos de fracciones equivalentes y el objetivo es seleccionar un representante que capture la esencia de todas las fracciones equivalentes, considerando factores como la simplicidad y la negatividad.
2.2 Equivalencia de vectores en el plano
Otro ejemplo de relaciones de equivalencia radica en la relación entre vectores en el plano. Los vectores fijos se consideran equivalentes si comparten la misma magnitud y dirección. La elección de un vector representativo, que normalmente se origina en el origen de coordenadas, ilustra el concepto de vector libre.
Habiendo establecido una base en las relaciones de equivalencia, el siguiente paso es introducir sin problemas la aritmética modular. Un punto de partida común es utilizar un ejemplo identificable, como los días de la semana, donde a cada día se le asigna un número del 0 (domingo) al 6 (sábado).
3.1 Días de la semana como ejemplo de aritmética modular
Al asignar números a los días de la semana y considerar una naturaleza cíclica, surge naturalmente la aritmética modular. Este ejemplo sirve como una ilustración tangible de los principios subyacentes a la aritmética modular, preparando el escenario para una exploración más profunda de sus aplicaciones en criptografía y criptografía de curva elíptica.
En los siguientes apartados profundizaremos en la mecánica de la aritmética modular, su aplicación en campos finitos y su papel para garantizar la seguridad de los sistemas criptográficos. Esta introducción, que cierra la brecha entre los conceptos teóricos y los ejemplos del mundo real, tiene como objetivo dotar a los estudiantes del conocimiento fundamental necesario para navegar por las complejidades de los algoritmos criptográficos.
En el ámbito de la criptografía, particularmente cuando se trata de curvas elípticas, se vuelve esencial una comprensión fundamental de la aritmética modular y los campos finitos. Esta introducción tiene como objetivo proporcionar a los estudiantes una comprensión fundamental de la aritmética modular, reconociendo su importancia en aplicaciones criptográficas dentro de campos finitos.
La necesidad de la aritmética modular
Las operaciones criptográficas que implican curvas elípticas suelen tener lugar dentro de un campo finito. Si bien los estudiantes de matemáticas e informática están familiarizados con las estructuras algebraicas, aquellos de ingeniería, ciencias y economía pueden requerir una introducción a la aritmética modular. A pesar de su posible complejidad, una comprensión básica es crucial para comprender los principios criptográficos dentro de campos finitos.
1. Relaciones de equivalencia: uniendo lo familiar y lo desconocido
El concepto de relaciones de equivalencia sirve como puerta de entrada a la aritmética modular. Ejemplos de contextos matemáticos cotidianos familiares para los estudiantes, como fracciones equivalentes y vectores en el plano, ayudan a cerrar la brecha entre la naturaleza abstracta de la aritmética modular y su conocimiento existente.
-1.1 Fracciones equivalentes: los estudiantes encuentran relaciones de equivalencia binaria cuando tratan con fracciones equivalentes. Elegir una fracción representativa de cada conjunto de equivalentes se vuelve análogo al proceso de selección dentro de la aritmética modular.
-1.2 Vectores en el plano: Similar a las fracciones equivalentes, la relación de equivalencia entre vectores implica seleccionar un vector representativo de cada conjunto con la misma magnitud y dirección. Este concepto allana el camino para comprender la aritmética modular a través de ejemplos familiares.
2. Introducción a la aritmética modular: ejemplo de días de la semana
Para iniciar la comprensión de la aritmética modular, se emplea un ejemplo práctico que involucra los días de la semana. Asignar números a cada día, desde el 0 (domingo) hasta las 6 (sábado), facilita la introducción de conceptos aritméticos modulares.
2.1 Definición de relaciones de equivalencia: Los números que representan días de la semana están relacionados módulo 7, lo que permite la identificación de conjuntos de números equivalentes. Esto forma la base de una relación de equivalencia binaria, denotada como
donde a — b es múltiplo de 7.
2.2 Conjunto de cocientes y notación: El conjunto de cocientes resultante, denotado como
(conjunto de números enteros módulo 7). Los elementos de este conjunto se representan numéricamente con una barra arriba:
-2.3 Operaciones en Z7 Las operaciones de suma y producto en Z7 se definen, enfatizando la reducción de resultados módulo 7. Este conjunto, junto con estas operaciones, exhibe la estructura de un campo.
3. Generalizar a Z7 y campos finitos
El proceso de aritmética modular se generaliza a cualquier número entero positivo. norteresultando en la introducción del conjunto cociente Z7. Para un entero positivo nortela relación de equivalencia binaria
está definido, y el cociente conjunto Z7 está establecido.
-3.1 Operaciones en Z7: Módulo de operaciones de suma y producto norte están definidos en Z7 En particular, para que cada elemento distinto de cero tenga una inversa, norte debe ser un número primo.
-3.2 Campos finitos FQ: El concepto de campos finitos. FQdónde q es el número de elementos, se introduce. Esto es particularmente relevante cuando norte es un número primo.
4. Cálculo de inversos y consideraciones prácticas
La introducción concluye describiendo el proceso de cálculo de inversas en aritmética modular, enfatizando la importancia de los elementos invertibles y proporcionando herramientas prácticas como el algoritmo euclidiano y el software Maxima.
En esta sección, exploramos las propiedades y operaciones asociadas con las curvas elípticas definidas en los números reales. Considere un polinomio cúbico
sin múltiples raíces. Una curva elíptica es el conjunto de puntos (x, y) que satisfacen la ecuación:
y² = x³ + ax + b
junto con un punto oh conocido como el punto del infinito.
Para obtener puntos en una curva elíptica se asignan valores reales a la incógnita X se sustituye en el lado derecho de la ecuación y se comprueba que el resultado sea un cuadrado en R (un número real mayor o igual a 0).
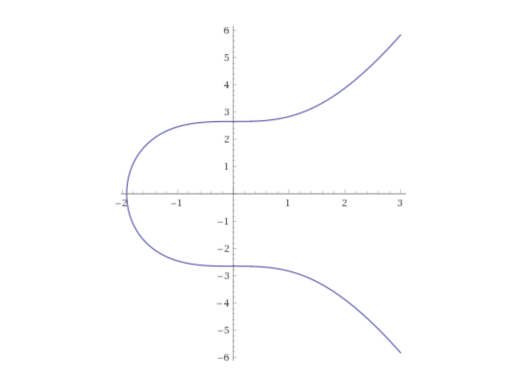
En el contexto de Bitcoin y blockchain, comúnmente se emplean curvas elípticas, específicamente la curva y² = x³ + 7.
Gráfica de una curva elíptica
En una curva elíptica, se define una operación de suma, donde el punto O sirve como elemento neutro P + O = O + P = P para cada punto P de la curva. Para dos puntos diferentes P y Q de la curva, su suma P + Q se obtiene de la siguiente manera:
1. Traza la recta r que pasa por los puntos P y Q.
2. La recta r corta la curva en otro punto; P + Q es el punto simétrico de este nuevo punto con respecto al eje x.
Doble de un punto
Para calcular 2P, la suma de un punto P consigo mismo:
1. Dibuja la recta tangente r a la curva en el punto P.
2. La recta r corta la curva en otro punto; 2P es el punto simétrico de este nuevo punto con respecto al eje x.
Siguiendo este proceso, el conjunto de puntos de una curva elíptica, con esta operación de suma, forma un grupo abeliano, satisfaciendo la propiedad asociativa y la existencia de un elemento neutro. oh y un elemento simétrico para cada punto.
Ecuaciones para operaciones de curva elíptica
Dados dos puntos
en una curva elíptica, la suma se calcula de la siguiente manera:
Estas expresiones proporcionan una representación analítica concisa para operaciones de curva elíptica, formando la base para las aplicaciones criptográficas en la tecnología blockchain.